Bagaimana Transformer Berfungsi

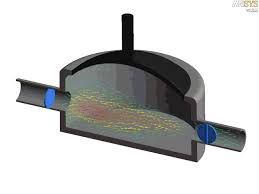
Mengikut definisi yang diberikan di Wikipedia pengubah elektrik adalah peralatan pegun yang bertukar kuasa elektrik melintasi beberapa gegelung yang luka rapat, melalui aruhan magnet.

Arus yang sentiasa berubah dalam satu belitan transformator menghasilkan fluks magnet yang berbeza-beza, yang, dengan itu, mendorong daya elektromotif yang berbeza-beza pada gegelung kedua yang dibina di atas teras yang sama.

Prinsip Kerja Asas

Transformer pada dasarnya berfungsi dengan mengalihkan kuasa elektrik di antara sepasang gegelung melalui induksi bersama, tanpa bergantung pada bentuk hubungan langsung antara kedua-dua belitan.

Proses pemindahan elektrik melalui induksi ini pertama kali dibuktikan oleh undang-undang induksi Faraday, pada tahun 1831. Menurut undang-undang ini, voltan teraruh di dua gegelung diciptakan disebabkan oleh fluks magnetik yang berbeza di sekitar gegelung.

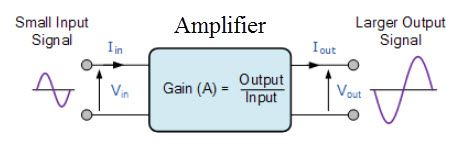
Fungsi asas pengubah adalah untuk menaikkan atau menurunkan voltan / arus bolak-balik, pada perkadaran yang berbeza mengikut keperluan aplikasi. Perkadaran ditentukan oleh bilangan putaran dan nisbah putaran belitan.

Menganalisis Transformer Ideal

Kita dapat membayangkan pengubah yang ideal untuk menjadi reka bentuk hipotesis yang mungkin hampir tanpa sebarang bentuk kerugian. Lebih-lebih lagi, reka bentuk yang ideal ini mungkin penggulungan primer dan sekundernya digabungkan dengan sempurna antara satu sama lain.

Artinya ikatan magnet antara dua belitan adalah melalui teras yang kebolehtelapan magnetiknya tidak terbatas, dan dengan induktansi belitan pada daya magnetomotif sifar keseluruhan.

Kita tahu bahawa dalam transformer, arus ulang-alik yang digunakan pada belitan primer cuba menegakkan fluks magnet yang berbeza di dalam teras transformer, yang juga merangkumi belitan sekunder yang dilingkari di sekelilingnya.

Oleh kerana fluks yang berbeza-beza ini, daya elektromotif (EMF) disebabkan pada belitan sekunder melalui aruhan elektromagnetik. Ini menghasilkan penghasilan fluks pada belitan sekunder dengan magnitud yang bertentangan tetapi sama dengan fluks belitan primer, menurut Undang-undang Lenz'z .

Oleh kerana inti membawa kebolehtelapan magnetik yang tidak terhingga, keseluruhan (100%) fluks magnet dapat dipindahkan merentasi kedua belitan.

Ini menyiratkan bahawa, ketika sumber utama terkena sumber AC, dan beban dihubungkan ke terminal penggulungan sekunder, arus mengalir melalui belitan masing-masing dalam arah seperti yang ditunjukkan dalam rajah berikut. Dalam keadaan ini daya magnetomotif teras dineutralkan menjadi sifar.

Gambar ihsan: https://commons.wikimedia.org/wiki/File:Transformer3d_col3.svg

Dalam reka bentuk transformer yang ideal ini, kerana pemindahan fluks di belitan primer dan sekunder adalah 100%, menurut undang-undang Faraday voltan yang diinduksi pada setiap belitan akan sebanding dengan jumlah putaran belitan, seperti yang ditunjukkan dalam berikut gambar:

Uji Video Mengesahkan Hubungan Linear antara Nisbah Giliran Utama / Sekunder.

RATIOS TURN DAN Tegangan

Mari cuba memahami pengiraan nisbah giliran secara terperinci:

Besarnya voltan yang disebabkan oleh belitan primer ke sekunder hanya ditentukan oleh nisbah bilangan lilitan luka pada bahagian primer dan sekunder.

Walau bagaimanapun, peraturan ini hanya berlaku jika pengubah berada dekat dengan pengubah yang ideal.

Transformer yang ideal adalah transformer yang mempunyai kerugian yang boleh diabaikan dalam bentuk kesan kulit atau arus eddy.

Mari kita ambil Contoh rajah 1 di bawah (untuk pengubah ideal).

Anggaplah belitan primer terdiri dari sekitar 10 putaran, sementara sekunder dengan belitan satu putaran. Oleh kerana aruhan elektromagnetik, garis fluks yang dihasilkan melintasi belitan primer sebagai tindak balas kepada input AC, secara bergantian mengembang dan runtuh, memotong 10 putaran belitan primer. Ini menghasilkan jumlah voltan yang tepat yang disebabkan oleh belitan sekunder bergantung pada nisbah putaran.

Penggulungan yang dibekalkan dengan input AC menjadi belitan utama, sementara belitan pelengkap yang menghasilkan output melalui aruhan magnet dari primer menjadi belitan sekunder.

Rajah 1)

Oleh kerana sekunder hanya mempunyai satu putaran, ia mengalami fluks magnetik berkadar melintasi satu putarannya berbanding dengan 10 putaran utama.

Oleh itu, kerana voltan yang dikenakan di seluruh primer adalah 12 V, maka setiap belitannya akan dikenakan EMF pembilang 12/10 = 1.2 V, dan ini adalah tepatnya voltan yang akan mempengaruhi putaran tunggal yang terdapat di seberang bahagian sekunder. Ini kerana ia mempunyai satu belitan yang hanya mampu mengeluarkan jumlah aruhan setara yang sama yang mungkin terdapat di satu putaran tunggal yang utama.

Oleh itu sekunder dengan satu putaran dapat mengeluarkan 1.2V dari yang utama.

Penjelasan di atas menunjukkan bahawa bilangan putaran pada primer pengubah sepadan secara linear dengan voltan bekalan di seberang dan voltan dibahagi dengan bilangan putaran.

Oleh itu, dalam kes di atas kerana voltan 12V, dan jumlah putaran adalah 10, EMF kaunter bersih yang disebabkan oleh setiap lilitan adalah 12/10 = 1.2V

Contoh # 2

Sekarang mari kita gambarkan gambar 2 di bawah, ia menunjukkan jenis konfigurasi yang serupa seperti pada gambar1. mengharapkan sekunder yang kini mempunyai 1 giliran tambahan, iaitu 2 nombor giliran.

Tidak perlu dikatakan, sekarang sekunder akan mengalami aliran fluks dua kali lebih banyak berbanding dengan keadaan angka 1 yang hanya mempunyai satu putaran.

Jadi di sini penggulungan sekunder akan dibaca sekitar 12/10 x 2 = 2.4V kerana kedua lilitan akan dipengaruhi oleh magnitud EMF kaunter yang mungkin setara di kedua belitan di sisi utama trafo.

Oleh itu dari perbincangan di atas secara umum kita dapat menyimpulkan bahawa dalam pengubah hubungan antara voltan dan bilangan lilitan merentasi primer dan sekunder agak linier dan berkadar.

Nombor Pusing Transformer

Oleh itu, formula yang diperoleh untuk mengira bilangan putaran bagi sebarang pengubah dapat dinyatakan sebagai:

Es / Ep = Ns / Np

di mana,

• Es = Voltan Sekunder ,
• Ep = Voltan Utama,
• Ns = Jumlah giliran sekunder,
• Np = Bilangan giliran Utama.

Nisbah Giliran Menengah Utama

Menarik untuk diperhatikan bahawa formula di atas menunjukkan hubungan langsung antara nisbah voltan sekunder ke voltan primer dan bilangan lilitan sekunder ke primer, yang ditunjukkan sebanding dan sama.

Oleh itu persamaan di atas juga dapat dinyatakan sebagai:

Ep x Ns = Es x Np

Selanjutnya, kita dapat memperoleh formula di atas untuk menyelesaikan Es dan Ep seperti yang ditunjukkan di bawah:

Es = (Ep x Ns) / Np

sama,

Ep = (Es x Np) / Ns

Persamaan di atas menunjukkan bahawa jika ada 3 magnitud yang ada, magnitud keempat dapat ditentukan dengan mudah dengan menyelesaikan rumus.

Menyelesaikan Masalah Penggulungan Transformer Praktikal

Kes pada titik # 1: Transformer mempunyai 200 bilangan lilitan di bahagian primer, 50 bilangan lilitan di sekunder, dan 120 volt disambungkan merentasi primer (Ep). Apakah voltan merentasi sekunder (E)?

Diberikan:

• Np = 200 giliran
• Ns = 50 giliran
• Ep = 120 volt
• Adakah =? voltan

Jawapan:

Es = EpN / Np

Mengganti:

Es = (120V x 50 putaran) / 200 giliran

Es = 30 volt

Kes pada titik # 2 : Katakan kita mempunyai 400 putaran wayar dalam gegelung teras besi.

Dengan andaian gegelung diperlukan untuk digunakan sebagai belitan utama pengubah, Hitung jumlah putaran yang perlu dililit pada gegelung untuk memperoleh belitan sekunder pengubah untuk memastikan voltan sekunder satu volt dengan keadaan di mana primer voltan ialah 5 volt?

Diberikan:

• Np = 400 giliran
• Ep = 5 volt
• Es = 1 volt
• Ns =? menoleh

Jawapan:

EpN = EsNp

Transposisi untuk Ns:

Ns = EsNp / Ep

Mengganti:

Ns = (1V x 400 putaran) / 5 volt

Ns = 80 giliran

Ingatlah: Nisbah voltan (5: 1) bersamaan dengan nisbah belitan (400: 80). Kadang-kadang, sebagai pengganti nilai tertentu, anda mendapati diri anda diberi nisbah putaran atau voltan.

Dalam kes seperti ini, anda boleh menganggap nombor sewenang-wenang untuk salah satu voltan (atau penggulungan) dan mencari nilai alternatif lain dari nisbah.

Sebagai gambaran, andaikan nisbah belitan ditugaskan sebagai 6: 1, anda dapat membayangkan jumlah giliran untuk bahagian utama dan mengetahui bilangan lilitan sekunder yang setara, menggunakan perkadaran yang serupa seperti 60:10, 36: 6, 30: 5, dll.

Transformer dalam semua contoh di atas membawa bilangan giliran yang lebih sedikit di bahagian sekunder berbanding bahagian utama. Atas sebab itu, anda dapat mencari voltan yang lebih kecil di sekunder trafo dan bukan di sisi utama.

Apa itu Transformer Step-up dan Step-Down

Transformer yang mempunyai penarafan voltan sisi sekunder lebih rendah daripada penarafan voltan sisi primer disebut sebagai a Pengubah STEP-DOWN .

Atau, sebagai alternatif jika input AC diterapkan pada belitan yang mempunyai bilangan putaran yang lebih tinggi maka transformer bertindak seperti pengubah step-down.

Nisbah transformer step-down empat hingga satu ditulis sebagai 4: 1. Transformer yang merangkumi bilangan putaran yang lebih sedikit di sisi primer berbanding dengan sisi sekunder akan menghasilkan voltan yang lebih tinggi di sisi sekunder berbanding dengan voltan yang disambungkan di sisi utama.

Transformer yang mempunyai sisi sekunder yang dinilai di atas voltan di sisi primer disebut sebagai pengubah STEP-UP. Atau, sebagai alternatif, jika input AC diaplikasikan pada belitan yang mempunyai bilangan putaran yang lebih rendah maka transformer bertindak seperti pengubah step-up.

Nisbah transformer tahap satu hingga empat perlu ditulis sebagai 1: 4. Seperti yang anda lihat dalam dua nisbah bahawa besarnya belitan sisi primer secara konsisten disebut pada awalnya.

Bolehkah kita Menggunakan Transformer Step-down sebagai Transformer Step-up dan Vice Versa?

Ya sememangnya! Semua transformer berfungsi dengan prinsip asas yang sama seperti yang dijelaskan di atas. Menggunakan transformer step-up sebagai transformer step-down bermaksud menukar voltan input merentasi belitan primer / sekundernya.

Sebagai contoh, jika anda mempunyai transformer step-up bekalan kuasa biasa yang memberi anda output 12-0-12V dari AC input 220V, anda boleh menggunakan transformer yang sama dengan transformer peningkatan untuk menghasilkan output 220V dari AC 12V input.

Contoh klasik ialah litar penyongsang , di mana pengubah tidak ada yang istimewa di dalamnya. Mereka semua menggunakan transformer step-down biasa yang disambungkan dengan cara yang bertentangan.

Kesan Beban

Setiap kali beban atau alat elektrik disambungkan ke lilitan sekunder pengubah, arus atau amp berjalan di sisi sekunder penggulungan bersama dengan beban.

Fluks magnet yang dihasilkan oleh arus dalam belitan sekunder berinteraksi dengan garis magnetik fluks yang dihasilkan oleh amp di sisi primer. Konflik antara kedua garis fluks ini dihasilkan sebagai hasil dari induktansi bersama antara belitan primer dan sekunder.

Flux Bersama

Fluks mutlak dalam bahan teras transformer berlaku pada belitan primer dan sekunder. Ini juga merupakan cara di mana kuasa elektrik dapat berpindah dari belitan primer ke belitan sekunder.

Kerana kenyataan bahawa fluks ini menyatukan kedua belitan, fenomena yang umumnya dikenali sebagai MUTUAL FLUX. Juga, induktansi yang menghasilkan fluks ini berlaku pada kedua-dua belitan dan disebut sebagai induktansi bersama.

Rajah (2) di bawah menunjukkan fluks yang dibuat oleh arus dalam belitan primer dan sekunder transformer setiap kali arus bekalan dihidupkan pada belitan primer.

Gambar (2)

Setiap kali rintangan beban disambungkan ke belitan sekunder, voltan yang dirangsang ke belitan sekunder memicu arus untuk beredar di belitan sekunder.

Arus ini menghasilkan cincin fluks di sekitar belitan sekunder (ditunjukkan sebagai garis putus-putus) yang mungkin sebagai alternatif untuk medan fluks di sekitar primer (hukum Lenz).

Akibatnya, fluks di sekitar belitan sekunder membatalkan sebahagian besar fluks di sekitar belitan primer.

Dengan jumlah fluks yang lebih kecil yang mengelilingi belitan utama, emf terbalik dikurangkan dan lebih banyak amp disedut dari bekalan. Arus tambahan dalam belitan utama melepaskan garis fluks tambahan, cukup banyak mengembalikan jumlah awal aliran fluks mutlak.

RATIOS TURNYA DAN SEMASA

Kuantiti garis fluks yang dihasilkan dalam teras trafo berkadar dengan daya magnet

(DI AMPERE-TURNS) dari belitan primer dan sekunder.

Giliran ampere (I x N) menunjukkan daya motif magneto yang dapat difahami sebagai daya magnetomotif yang dihasilkan oleh satu ampere arus yang berjalan dalam gegelung 1 putaran.

Fluks yang terdapat di teras pengubah mengelilingi belitan primer dan sekunder.

Memandangkan fluks sama untuk setiap belitan, putaran ampere pada setiap belitan primer dan sekunder harus selalu sama.

Untuk tujuan itu:

IpNp = IsNs

Di mana:

IpNp = ampere / putaran pada penggulungan utama
IsNs - ampere / putaran pada penggulungan sekunder

Dengan membahagikan kedua-dua sisi ungkapan dengan
Ip , kita mendapatkan:
Np / Ns = Is / Ip

sejak: Es / Ep = Ns / Np

Kemudian: Ep / Es = Np / Ns

Juga: Ep / Es = Adakah / Ip

di mana

• Ep = voltan digunakan pada voltan utama dalam volt
• Es = voltan merentasi sekunder dalam volt
• Ip = semasa di sekolah rendah di Amp
• Is = semasa di sekunder di Amps

Perhatikan bahawa persamaan menunjukkan nisbah ampere menjadi kebalikan dari belitan atau nisbah putaran serta nisbah voltan.

Ini menunjukkan, pengubah yang mempunyai bilangan putaran yang lebih sedikit di sisi sekunder berbanding yang utama mungkin menurunkan voltan, tetapi ia akan meningkatkan arus. Contohnya:

Pengubah yang mempunyai nisbah voltan 6: 1.

Cuba cari arus atau amp di sisi sekunder jika arus atau amp di sisi utama ialah 200 miliamper.

Andaikan

Ep = 6V (sebagai contoh)
Adakah = 1V
Ip = 200mA atau 0.2Amps
Adakah =?

Jawapan:

Ep / Es = Adakah / Ip

Transposisi untuk Adalah:

Adakah = EpIp / Es

Mengganti:

Is = (6V x 0.2A) / 1V
Adakah = 1.2A

Senario di atas menunjukkan bahawa walaupun voltan merentasi belitan sekunder adalah satu perenam voltan melintasi belitan primer, amp di belitan sekunder adalah 6 kali amp di belitan primer.

Persamaan di atas dapat dilihat dengan baik dari perspektif alternatif.

Nisbah belitan menandakan jumlah di mana pengubah meningkatkan atau meningkatkan atau mengurangkan voltan yang disambungkan ke sisi utama.

Sebagai gambaran saja, andaikan jika belitan sekunder transformer mempunyai bilangan putaran dua kali ganda berbanding belitan primer, voltan yang dirangsang ke sisi sekunder mungkin akan dua kali ganda voltan melintasi belitan primer.

Sekiranya belitan sekunder membawa satu setengah bilangan lilitan sisi utama, voltan di sisi sekunder akan menjadi setengah voltan melintasi belitan utama.

Oleh itu, nisbah belitan bersama dengan nisbah amp transformer terdiri daripada persatuan terbalik.

Akibatnya, transformer step-up 1: 2 dapat mempunyai setengah amp di sisi sekunder dibandingkan dengan sisi utama. Transformer step-down 2: 1 boleh mempunyai dua kali amp pada belitan sekunder yang berkaitan dengan sisi utama.

Ilustrasi: Transformer dengan nisbah belitan 1:12 mempunyai arus 3 ampere di sisi sekunder. Ketahui besarnya amp dalam belitan utama?

Diberikan:

Np = 1 giliran (misalnya)
Ns = 12 giliran
Adakah = 3Amp
Lp =?

Jawapan:

Np / Ns = Is / Ip

Mengganti:

Ip = (12 putaran x 3 Amp) / 1 giliran

Ip = 36A

Mengira Induktansi Saling

Induksi bersama adalah proses di mana satu penggulungan melalui induksi EMF kerana kadar arus perubahan belitan bersebelahan yang membawa kepada gandingan induktif antara belitan.

Dalam kata lain Induktansi Saling adalah nisbah emf yang diinduksi pada satu belitan dengan kadar perubahan arus pada belitan yang lain, seperti yang dinyatakan dalam formula berikut:

M = emf / di(t) / dt

Fasa dalam Transformer:

Lazimnya, semasa kita memeriksa transformer, kebanyakan kita percaya bahawa voltan dan arus belitan primer dan sekunder berada dalam fasa satu sama lain. Walau bagaimanapun, ini mungkin tidak selalu benar. Dalam transformer, hubungan antara voltan, sudut fasa semasa merentasi primer dan sekunder bergantung pada bagaimana belitan ini dipusingkan pada teras. Itu bergantung pada apakah keduanya berada dalam arah berlawanan arah jarum jam, atau arah searah jarum jam atau mungkin satu belitan dipusingkan mengikut arah jam sementara yang lain berliku berlawanan arah jam.

Mari rujuk gambar rajah berikut untuk memahami bagaimana orientasi belitan mempengaruhi sudut fasa:

Dalam contoh di atas, arah belitan kelihatan sama, iaitu kedua-dua belitan primer dan sekunder dipusingkan mengikut arah jam. Oleh kerana orientasi yang sama ini, sudut fasa arus keluaran dan voltan sama dengan sudut fasa arus input dan voltan.

Dalam contoh kedua di atas, arah penggulungan pengubah dapat dilihat luka dengan arah yang berlawanan. Seperti yang dapat dilihat, primer nampaknya searah jarum jam sementara yang kedua dililit berlawanan arah jarum jam. Oleh kerana orientasi penggulungan berlawanan ini, sudut fasa antara kedua belitan berjauhan 180 darjah, dan output sekunder yang diinduksi menunjukkan arus fasa keluar dan tindak balas voltan.

Dot Notation dan Dot Convention

Untuk mengelakkan kekeliruan, notasi Dot atau konvensi Dot digunakan untuk mewakili orientasi belitan transformer. Ini membolehkan pengguna memahami spesifikasi sudut fasa input dan output, sama ada belitan primer dan sekunder dalam fasa atau di luar fasa.

Konvensyen titik dilaksanakan dengan tanda titik di seluruh titik permulaan penggulungan, yang menunjukkan sama ada penggulungan berada dalam fasa atau tidak fasa antara satu sama lain.

Skema transformer berikut membawa denotasi konvensyen dot, dan ini menandakan bahawa primer dan sekunder transformer berada dalam fasa satu sama lain.

Notasi titik yang digunakan dalam ilustrasi di bawah menunjukkan DOT diletakkan di seberang titik berlawanan primer dan penggulungan sekunder. Ini menunjukkan bahawa orientasi belitan kedua sisi tidak sama dan oleh itu sudut fasa melintasi dua belitan akan 180 darjah keluar dari fasa apabila input AC diterapkan pada salah satu belitan.

Kerugian dalam Transformer Sebenar

Pengiraan dan formula yang dipertimbangkan dalam perenggan di atas didasarkan pada transformer yang ideal. Namun dalam dunia nyata, dan untuk pengubah sebenar, senario mungkin jauh berbeza.

Anda akan dapati bahawa dalam reka bentuk yang ideal faktor linier asas transformer sebenar akan diabaikan:

(a) Banyak jenis kerugian Teras, yang bersama-sama dikenali sebagai magnetisasi kerugian semasa, yang mungkin termasuk jenis kerugian berikut:

• Kerugian histeresis: ini disebabkan oleh pengaruh nonlinier fluks magnet pada teras pengubah.
• Kerugian arus Eddy: Kerugian ini disebabkan oleh fenomena yang disebut pemanasan joule di teras pengubah. Ia berkadaran dengan kuasa dua voltan yang dikenakan pada primer pengubah.

(b) Berbeza dengan transformer yang ideal, rintangan belitan dalam transformer sebenar tidak boleh mempunyai rintangan sifar. Bererti penggulungan akhirnya akan mempunyai beberapa rintangan dan induktansi yang berkaitan dengannya.

• Kerugian Joule: Seperti yang dijelaskan di atas, Rintangan yang dihasilkan di terminal penggulungan menimbulkan kerugian Joule.
• Fluks kebocoran: Kami tahu bahawa transformer sangat bergantung pada aruhan magnetik di seluruh belitannya. Walau bagaimanapun, kerana belitan dibina pada teras tunggal yang sama, fluks magnet menunjukkan kecenderungan bocor melintasi belitan melalui inti. Ini menimbulkan impedans yang disebut impedans reaktif primer / sekunder, yang menyumbang kepada kerugian pengubah.

(c) Oleh kerana pengubah juga sejenis induktor, ia juga dipengaruhi oleh fenomena seperti kapasitansi parasit dan resonans diri, kerana pengedaran medan elektrik. Kapasitansi parasit ini biasanya dapat dalam 3 bentuk yang berbeza seperti yang diberikan di bawah:

• Kapasiti yang dihasilkan antara giliran satu di atas yang lain di dalam satu lapisan
• Kapasiti dihasilkan di dua atau lebih lapisan bersebelahan
• Kapasiti dibuat antara teras pengubah dan lapisan penggulungan yang terletak bersebelahan dengan teras

Kesimpulannya

Dari perbincangan di atas, kita dapat memahami bahawa dalam aplikasi praktikal mengira transformer, terutamanya transformer teras besi mungkin tidak semudah transformer ideal.

Untuk mendapatkan hasil yang paling tepat untuk data penggulungan, kita mungkin perlu mempertimbangkan banyak faktor seperti: ketumpatan fluks, luas teras, ukuran teras, lebar lidah, kawasan tingkap, jenis bahan teras dll.

Anda boleh mengetahui lebih lanjut mengenai semua pengiraan ini di bawah siaran ini: